- НМТ 2024. 2log63 + log64=
А Б В Г Д log610 log624 log613 2 6 Відповідь
Г. - НМТ 2024. Укажіть проміжок, якому належить значення виразу log0,2125.
А Б В Г Д (–∞; –3) [–3; 0) [0; 3) [3; 25) [25; +∞) Відповідь
Б. Звести числа до степенів з основою 5. - НМТ 2023. До початку речення (1-3) доберіть закінчення (А-Д) так, щоб утворилося правильне твердження, якщо n - натуральне число.
Початок речення Закінчення речення 1 Якщо , то
2 Якщо 1+log3n=log3a, то
3 Якщо 3n ⋅3=3a, тоА a=3n
Б a=n+1
В a=n+3
Г
ДВідповідь
1-Д, 2-А, 3-Б. - Обчисліть log816.
А Б В Г Д 1 8 12 Відповідь
Б.
Представити числа у вигляді степенів числа 2. - log25+log21,6 =
А Б В Г Д 3 3,3 0,25 4 log26,6 Відповідь
А.
Скористатись формулою суми логарифмів. - Обчисліть значення виразу log549+2log5
.
А Б В Г Д 0 1 2 4 25 Відповідь
В.
Скористатись формулою суми логарифмів. - Обчисліть значення виразу log345+log3900-log3500.
А Б В Г Д 4 3 27 log3445 Відповідь
Б.
Скористатись формулами суми та різниці логарифмів. -
А Б В Г Д lg5 5 lg20 2 0,5 Відповідь
Г.
Представити 25 як степінь числа 5. - Обчисліть
.
А Б В Г Д 5 6 10 25 36 Відповідь
Г.
Представити 36 як степінь числа 6. - Якщо log43 = a, то log169 = ?
А Б В Г Д 4a а2 2a a Відповідь
Д.
Представити числа у вигляді степенів. - Обчисліть
, якщо logab = 7.
А Б В Г Д 2 3 4 Відповідь
Д.
Перетворити корінь квадратний на степінь. - Укажіть проміжок, якому належить число log54.
А Б В Г Д (0;1) (1;2) (2;3) (3;4) (4;5) Відповідь
А.
Обмежити 4 числами, що є степенями числа 5. - Укажіть проміжок, якому належить число log29.
А Б В Г Д (0;1) (1;2) (2;3) (3;4) (4;5) Відповідь
Г.
Обмежити 9 числами, що є степенями числа 2. - 2019. Якому з наведених проміжків належить число
А Б В Г Д (-∞;-3) (-3;-1) (-1;1) (1;3) (3;+∞) Відповідь
Б.
Обмежити 1/3 числами, що є степенями числа 2. - До кожного виразу (1-4) оберіть тотожно йому рівний (А-Д), якщо m>2, m - натуральне число.
Вираз Тотожно рівний вираз 1 (m+1)2-m2-1
2 mcos2α+ msin2α
3 100lgm
4А 0
Б m
В 2m
Г m2
ДВідповідь
1-В, 2-Б, 3-Г, 4-Д .
1) Скористатись формулою скороченого множення.
2) Винести m за дужки.
3) Представити 100 у вигляді степеня числа 10.
4) Представити корінь у вигляді степеня. - 2019. Установіть відповідність між виразом (1-4) та тотожно рівним йому виразом (А-Д), якщо а>0,а≠1,m≠0, n≠0, m≠ -n.
Вираз Тотожно рівний вираз 1
2
3
4 n(6m+1)-m(6n-1)А mn
Б
В
Г n+m
Д n-mВідповідь
1-Д, 2-Б, 3-В, 4-Г.
1) Скористатись формулою скороченого множення.
2) Перетворити ділення на множення
3) Винести степені за логарифм.
4) Розкрити дужки. - 2019. Нехай а — довільне додатне число. Установіть відповідність між виразом (1-4) та тотожно рівним йому виразом (А-Д).
Вираз Тотожно рівний вираз 1 a-1
2
3
4 25log5aА -a
Б
В a
Г a2
Д 25aВідповідь
1-Б, 2-В, 3-Д, 4-Г.
3)Перетворити ділення на множення.
4) Представити 25 як степінь числа 5. - Установіть відповідність між виразом (1-4) та тотожно рівним йому виразом (А-Д), якщо а — довільне додатне число.
Вираз Тотожно рівний вираз 1 (3a3)2
2
3
4 32+log3a3А 9a6
Б 9a3
В 9a5
Г 3a3
Д 3a2Відповідь
1-А, 2-Д, 3-Г, 4-Б.
4) Скористатись формулою добутку степенів з однаковою основою. - До кожного початку речення (1-4), де а>0, b>0, доберіть його закінчення (А-Д) так, щоб утворилося правильне твердження.
Початок речення Закінчення речення 1 Якщо log2a = 2log2b, то
2 Якщо a3 = 8b3, то
3 Якщо, то
4 Якщо 2a = 4·2b, тоА a = 2b
Б a = 2+b
В a = 4b
Г a = b2
Д a = 3bВідповідь
1-Г, 2-А, 3-В, 4-Б.
1-4) Звести ліві та праві частини рівностей до однакового вигляду. - 2021. Обчисліть 4001-log204.
Відповідь
25.
Скористатись формулою частки степенів з однаковою основою. - Обчисліть значення виразу
Відповідь
4,9. - Обчисліть значення виразу loga500-loga4, якщо
Відповідь
12.
Скористатись формулою різниці логарифмів. - Обчисліть log2
+log525.
Відповідь
-1.
Обчислити значення логарифмів. - Обчисліть log318-log32.
Відповідь
2.
Скористатись формулою різниці логарифмів з однаковою основою. - Обчисліть значення виразу
.
Відповідь
0,5.
Звести до однакових степенів і винести степінь за дужки. - Обчисліть log328-
.
Відповідь
-48,4.
Поміняти місця основу та підлогарифмічний вираз у степені. - Обчисліть
.
Відповідь
80.
Скористатись формулою добутку степенів з однаковою основою. - Обчисліть
.
Відповідь
1,68.
Скористатись формулою добутку степенів з однаковою основою. - Якщо додатні числа х і у задовольняють умову
, то
1.=
2. log2x-log2y =Відповідь
1,25; -2.
1. Розкласти на два дроби
2. Скористатись формулою різниці логарифмів з однаковою основою.
Дії з логарифмами
Якщо logab = c, то b = ac
logaa = 1
loga1 = 0
logab+logac = logabc
logab-logac = loga
n⋅logab = logabn
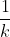 logab = logakb
logab = logakb
alogaN = N
Якщо logab = c, то b = ac
logaa = 1
loga1 = 0
logab+logac = logabc
logab-logac = loga
n⋅logab = logabn
alogaN = N
Правильну відповідь можна дізнатися, натискаючи кнопку Відповідь під завданням. Послуга ознайомлення з повними розв’язаннями завдань з цієї теми коштує 120 грн. Для отримання цієї послуги надішліть зі своєї електронної пошти листа на адресу ssychov@gmail.com з вказівкою теми "1.6. Логарифмічні вирази". У відповідь Вам надійде розрахунковий рахунок для переказу коштів. Після оплати надішліть скріншот квитанції і на Вашу адресу надійдуть розв’язки у pdf-форматі. Для перегляду зразка розв’язання натисніть кнопку нижче.

що за магія в 25 коли з кореня (14) + 05 стало 14+1?
ВідповістиВидалитиВираз log3(корінь14)+0,5 був у дужках, перед якими стояло 2. При розкритті дужок отримали 2log3(корінь14)+2*0,5. 2 перед логарифмом заносимо в степінь кореня, 2*0,5=1. Тому і отримуємо log3(14)+1
Видалити