Шлях до математики: кроки успіху: НМТ - 2024

1:00:00

На цій сторінці Ви маєте можливість перевірити свою можливість виконати тестове завдання з НМТ на час. Вам надається 60 хв (орієнтовний час виконання завдання з математики при рівному розподілу часу на українську мову та математику).

Зверніть увагу! Якщо у завданнях 19-22 дробові відповіді треба записувати десятковим дробом, розділяючи цілу та дробову частину КОМОЮ.

Для початку тестування натисність кнопку

Орієнтовний час на виконання завдань з математики вичерпано. Якщо бажаєте отримати результат, натисніть кнопку 'Перейти до результату'. Якщо бажаєте продовжити виконання тесту за рахунок зменшення часу на українську мову, натисніть кнопку 'Продовжити роботу'

1. У салоні пасажирського літака 20 рядів, у кожному з яких розташовано по 3 крісла обабіч проходу (див. рисунок). Реєструючи пасажира, електронна система навмання вибирає для нього посадкове місце. Яка імовірність того, що першому зареєстрованому пасажиру дістанеться місце біля проходу?

А	Б	В	Г	Д
$\frac{1}{2}$	$\frac{1}{6}$	$\frac{1}{3}$	$\frac{2}{3}$	$\frac{1}{120}$

А
Б
В
Г
Д

2. (4x − 5)² =

А	Б	В	Г	Д
16x² − 40x + 25	16x² − 25	16x² − 20x + 25	16x² + 25	4x² − 40x + 25

А
Б
В
Г
Д

3. Яке з наведених чисел є розв’язком нерівності |−2x − 3| > 5?

А	Б	В	Г	Д
–2	–1	0	1	2

А
Б
В
Г
Д

4. Відомо, що вісь AO Пізанської вежі натепер відхилена від вертикалі BO на кут 4^o (див. рисунок). Визначте градусну міру кута AOC, який утворює вісь вежі з горизонтальною поверхнею OC.

А	Б	В	Г	Д
176^o	94^o	104^o	86^o	96^o

А
Б
В
Г
Д

5. На рисунку зображено куб ABCDA₁B₁C₁D₁. Укажіть із-поміж наведених пряму, паралельну площині грані AA₁B₁B.

А	Б	В	Г	Д
BC	C₁D	BD	CB₁	A₁B

А
Б
В
Г
Д

6. Графік однієї з наведених функцій проходить через точку, зображену на рисунку. Укажіть цю функцію.

А	Б	В	Г	Д
y = log₄x	$y=\sqrt{x}$	y = x + 2	y = −x²	$y=\frac{1}{x}$

А
Б
В
Г
Д

7. Маса протона наближено дорівнює 1,67 ∙ 10⁻²⁷ кг. Визначте наближену масу (кг) 100 протонів.

А	Б	В	Г	Д
167 ∙ 10⁻²⁵	1,67 ∙ 10⁻²⁵	1,67 ∙ 10⁻²⁹	1,67 ∙ 10⁻²⁷⁰⁰	1,67 ∙ 10²⁵

А
Б
В
Г
Д

8. Основою піраміди є ромб, діагоналі якого дорівнюють 20 см і 12 см. Обчисліть об’єм (см³) піраміди, якщо її висота дорівнює 15 см.

А	Б	В	Г	Д
1800	1200	2400	800	600

А
Б
В
Г
Д

9. Обчисліть значення виразу $2\sqrt{m+m+m}$ , якщо $m=\frac{1}{27}$ .

А	Б	В	Г	Д
$\frac{2}{3}$	6	$\frac{1}{6}$	$\frac{3}{2}$	$\frac{2}{9}$

А
Б
В
Г
Д

10. Які з наведених тверджень є правильними?
І. Cерединний перпендикуляр, проведений до сторони рівностороннього трикутника, ділить його на два рівних трикутники.
ІІ. Точка перетину серединних перпендикулярів, проведених до катетів прямокутного трикутника, є серединою його гіпотенузи.
ІІІ. Точка перетину серединних перпендикулярів, проведених до сторін будь-якого тупокутного трикутника, міститься всередині цього трикутника.

А	Б	В	Г	Д
лише І	лише І та ІІ	лише І та ІІІ	лише IІ та ІІІ	І, ІІ та ІІІ

А
Б
В
Г
Д

11. Розв’яжіть систему рівнянь $\begin{cases}2x-\frac{y}{3} = 7,\\4x+\frac{2y}{3}=6\end{cases}$ . Якщо (x₀;y₀) - розв'язок системи, то x₀+y₀=

А	Б	В	Г	Д
–3,5	4,5	6	-4	10,5

А
Б
В
Г
Д

12. Сума перших п’яти членів геометричної прогресії (b_n) дорівнює 32, а сума перших чотирьох її членів дорівнює 20. Визначте b₅.

А	Б	В	Г	Д
1,6	52	11,4	–12	12

А
Б
В
Г
Д

13. 2log₆3 + log₆4=

А	Б	В	Г	Д
log₆10	log₆24	log₆13	2	6

А
Б
В
Г
Д

14. Розв’яжіть рівняння $3^{x^2}=81$ . Якщо рівняння має один корінь, то вкажіть проміжок, якому він належить. Якщо рівняння має кілька коренів, то вкажіть проміжок, якому належить найменший з них.

А	Б	В	Г	Д
(–∞; –10)	[–10; –3)	[–3; –2)	[–2; 0)	[0; +∞)

А
Б
В
Г
Д

15. На стороні AD паралелограма ABCD вибрано точку K так, що AK : KD = 3 : 2, BK = CD (див. рисунок). Визначте площу паралелограма ABCD, якщо ∠AKB = α, BC = 20.

А	Б	В	Г	Д
$\frac{120}{tg\alpha}$	120tgα	160sinα	60cosα	$\frac{60}{tg\alpha}$

А
Б
В
Г
Д

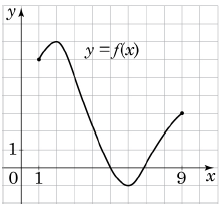
16. На рисунку зображено графік функції y = f(x), визначеної на відрізку [1; 9]. Доберіть до початку речення (1–3) його закінчення (А − Д) так, щоб утворилося правильне твердження.

Початок речення	Закінчення речення
1 Найбільше значення функції y = f(x) на відрізку [1; 9] дорівнює 2 Найменше значення функції y = f(x) на відрізку [1; 3] дорівнює 3 Найбільше ціле значення x, за якого справджується нерівність f(x)<0, дорівнює	А −1. Б 9. В 6. Г 7. Д 5.

17. Узгодьте вираз (1–3) із твердженням (А − Д) щодо значення цього виразу.

Вираз	Твердження про значення виразу
1 $\frac{\pi}{3}$ 2 $sin(\frac{7\pi}{2})$ 3 $\pi^{cos90^o}$	А є ірраціональним числом Б є натуральним числом В є цілим від’ємним числом Г є раціональним числом, що не є цілим Д дорівнює 0

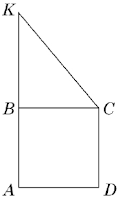
18.Трапеція AKCD складається з квадрата ABCD та трикутника BKC (див. рисунок). Периметр квадрата ABCD дорівнює 24 см, середня лінія трапеції AKCD дорівнює 10 см. До кожного початку речення (1–3) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження.

Початок речення	Закінчення речення
1 Довжина відрізка BK дорівнює 2 Довжина відрізка KC дорівнює 3 Відстань між центрами кіл, описаних навколо квадрата ABCD та трикутника BKC, дорівнює	А 8 см. Б 7 см. В 6 см. Г 10 см. Д 12 см.

19. На рисунку зображено графік функції $f(x) =\begin{cases}1,x\in (-\infty ;0],\\2,x\in (0;+\infty).\end{cases}$ Обчисліть значення виразу $\int_{-4}^{-1}f(x)dx + 2\int_{1}^{8}f(x)dx$ .

20. Заступник директора школи складає розклад уроків для 10-го класу. Він запланував на понеділок шість уроків з таких предметів: геометрія, біологія, англійська мова, хімія, фізична культура, географія. Скільки всього існує різних варіантів розкладу уроків на цей день, якщо урок фізичної культури має бути першим або останнім у розкладі?

21. У прямокутній системі координат у просторі задано конус із вершиною M(4; −9; 7). Осьовим перерізом цього конуса є рівносторонній трикутник AMB. Визначте площу S повної поверхні цього конуса, якщо A(8; −12; 12). У відповіді запишіть значення $\frac{S}{\pi}$ .