Шлях до математики: кроки успіху: 7 клас. Алгебра. Графік функції

Графіком функції називають фігуру, що складається з усіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати дорівнюють відповідним значенням функції.

Алгоритм побудови графіку довільної функції:

Скласти таблицю значень функції для певної кількості значень аргументу (чим більше значень аргументу, тим точніше буде будуватися графік).
Позначити точки, координати яких подано в таблиці, на координатній площині.
Сполучити точки плавною лінією.

Характеристики графіка функції:

Область визначення функції. Для неперервної функції це ліва та права межа графіка по осі абсцис (вісь х)
Область значень функції. Для неперервної функції це нижня та верхня межа графіка по осі ординат (вісь у)
Нуль функції. Нулем функції є абсциса (х, перша координата) точки перетину графіка функції з віссю абсцис (вісь х).

Оскільки за означенням функції кожному значенню незалежної змінної відповідає єдине значення залежної змінної, то якщо на фігурі на координатній площині якомусь значенню х відповідає декілька значень у, то така фігура не є графіком функції.

Для перевірки чи належить дана точка графіку функції (графік функції проходить ерез дану точку) треба підставити в рівняння функції замість аргумента значення абсциси точки і порівняти отримане значення функції з ординатою точки. Якщо значення функції та ордината точки спіпадають, то точка належить графіку функції. Якщо не співпадають, то точка графіку функції не належить.

Приклади

Скласти таблицю для цілих значень аргументу функції y = 2x – 1, де –3 ≤ х ≤ 4 і побудувати графік.
Розв'язування
y(-3) = 2 ⋅ (-3) - 1 = - 6 - 1 = - 7.
y(-2) = 2 ⋅ (-2) - 1 = - 4 - 1 = - 5.
y(-1) = 2 ⋅ (-1) - 1 = - 2 - 1 = - 3.
y(0) = 2 ⋅ 0 - 1 = 0 - 1 = - 1.
y(1) = 2 ⋅ 1 - 1 = 2 - 1 = 1.
y(2) = 2 ⋅ 2 - 1 = 4 - 1 = 3.
y(3) = 2 ⋅ 3 - 1 = 6 - 1 = 5.
y(4) = 2 ⋅ 4 - 1 = 8 - 1 = 7.

x -3 -2 -1 0 1 2 3 4

y -7 -5 -3 -1 1 3 5 7

Графік функції:
Порядок побудови:
Скласти таблицю для цілих значень аргументу функції y = x² – 2, де –3 ≤ х ≤ 3 і побудувати графік.
Розв'язування
y(-3) = (-3)² - 2 = 9 - 2 = 7.
y(-2) = (-2)² - 2 = 4 - 2 = 2.
y(-1) = (-1)² - 2 = 1 - 2 = - 1.
y(0) = 0² - 2 = 0 - 2 = - 2.
y(1) = 1² - 2 = 1 - 2 = - 1.
y(2) = 2² - 2 = 4 - 2 = 2.
y(3) = 3² - 2 = 9 - 2 = 7.

x -3 -2 -1 0 1 2 3

y 7 2 -1 -2 -1 2 7

Графік функції:
Порядок побудови:
Встановіть, чи належить графіку функції у = 3х - 4 точки А(2;8) і В(1;-1).
Розв'язування
А(2;8)
Підставимо замість аргумента функції х абсцису точки А.
y(2) = 3 ⋅ 2 - 4 = 6 - 4 = 2. Отримане значення не співпадає з ординатою точки А (2≠8), тому точка А не належить графіку функції.
В(1;-1)
Підставимо замість аргумента функції х абсцису точки В.
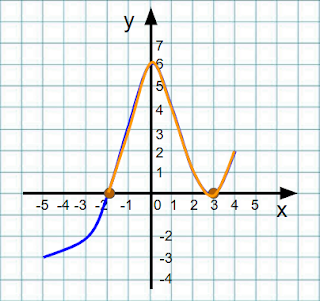
y(1) = 3 ⋅ 1 - 4 = 3 - 4 = -1. Отримане значення співпадає з ординатою точки В, тому точка В належить графіку функції.
За графіком, який зображено на малюнку, знайдіть:

область визначення функції;

область значень функції;

значення у, якщо х = - 3;

значення x, якщо y = 2;

нулі функції;

значення аргументу, за яких функція набуває додатних значень

значення аргументу, за яких функція набуває від'ємних значень

Розв'язування
1. Аргумент функції змінюється від -5 до 4. Тому область визначення функції –5 ≤ х ≤ 4.
2. Значення функції змінюється від -3 до 6. Тому область значень функції –3 ≤ у ≤ 6.
3. За малюнком, якщо х = -3, то у = - 2.
4. За малюнком, якщо у = 2, то х≈- 1,3; х≈1,6 та х = 4.
5. Графік функції перетинає вісь абсцис у точках (-2;0) та (3;0). Тому нулі функції: х = -2 та х = 3.
6. За малюнком функція набуває додатних значень там, де графік функції лежить вище осі х. Маємо –2 < x < 3 та при 3 < x ≤ 4.
7. За малюнком функція набуває від'ємних значень там, де графік функції лежить нижче осі х. Маємо –5 ≤ x < -2.