Координати у просторі — основа аналітичної геометрії, що дозволяє описувати положення будь-якої точки за допомогою трійки чисел (x; y; z). На цій сторінці ми розберемо ключові поняття: розташування точок на координатних осях і площинах, обчислення відстані між точками та знаходження центру відрізка.
Особливу увагу приділено рівнянню сфери та розв'язанню практичних завдань. Ви знайдете покрокові пояснення до задач НМТ минулих років, включаючи складні комплексні завдання. Ці матеріали допоможуть вам структурувати знання та навчитися швидко знаходити правильні відповіді на іспиті!
Координати точки
Завдання 1. У прямокутній системі координат у просторі задано правильну чотирикутну призму ABCDA₁B₁C₁D₁. Діагоналі основи ABCD перетинаються в точці M. Висота призми втричі більша за сторону AB. Обчисліть об’єм цієї призми, якщо A(4; √10; 3), M(–2; 0; 1).
- Якщо точка належить осі ОХ, то вона має координати (х;0;0), якщо точка належить осі ОУ, то вона має координати (0;у;0), якщо точка належить осі ОZ, то вона має координати (0;0;z)
- Якщо точка належить площині ОХУ, то вона має координати (х;у;0), якщо точка належить площині ОУZ, то вона має координати (0;у;z), якщо точка належить площині ОХZ, то вона має координати (х;0;z)
- Відстань між точками А(хA;yA;zA) та B(хB;yB;zB) знаходять за формулою AB = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2 + (z_B-z_A)^2}
- Координати точки О, яка є серединою відрізка АВ, знаходять за формулами: хₒ = \frac{x_A + x_B}{2}, yₒ = \frac{y_A + y_B}{2}, zₒ = \frac{z_A + z_B}{2}
Показати відповідь
3000.
Знайдемо довжину відрізка AM (половина діагоналі основи). AМ = \sqrt{(x_M-x_A)^2 + (y_M-y_A)^2 + (z_M-z_A)^2} = \sqrt{(-2-4)^2 + (0-\sqrt{10})^2 + (1-3)^2} = \sqrt{(-6)^2 + (-\sqrt{10})^2 + (-2)^2} = \sqrt{36 + 10 + 4} = \sqrt{50} = 5\sqrt{2}. Тоді діагональ AC = 2 · AM = 10\sqrt{2}. Так як діагональ квадрата d = a√2, то АВ = 10\sqrt{2}:\sqrt{2} = 10. Знайдемо висоту. За умовою H = 3 · AB = 3 · 10 = 30. V = Sосн · H = 10² · 30 = 100 · 30 = 3000.
Знайдемо довжину відрізка AM (половина діагоналі основи). AМ = \sqrt{(x_M-x_A)^2 + (y_M-y_A)^2 + (z_M-z_A)^2} = \sqrt{(-2-4)^2 + (0-\sqrt{10})^2 + (1-3)^2} = \sqrt{(-6)^2 + (-\sqrt{10})^2 + (-2)^2} = \sqrt{36 + 10 + 4} = \sqrt{50} = 5\sqrt{2}. Тоді діагональ AC = 2 · AM = 10\sqrt{2}. Так як діагональ квадрата d = a√2, то АВ = 10\sqrt{2}:\sqrt{2} = 10. Знайдемо висоту. За умовою H = 3 · AB = 3 · 10 = 30. V = Sосн · H = 10² · 30 = 100 · 30 = 3000.
Завдання 2. Яка з наведених точок належить осі Оz прямокутної системи координат у просторі?
М(0;-3;0)
N(3;0;-3)
K(-3;0;0)
L(-3;3;0)
F(0;0;-3)
Показати відповідь
Д.
Оскільки точка належить осі Оz, то в неї координати х та у дорівнюють 0. Цій умові задовольняє лише точка F.
Завдання 3. У прямокутній декартовій системі координат у просторі на осі z вибрано точку М (див. рисунок). Серед наведених варіантів укажіть можливі координати цієї точки.
Оскільки точка належить осі Оz, то в неї координати х та у дорівнюють 0. Цій умові задовольняє лише точка F.
(1;0;0)
(1;1;0)
(0;0;1)
(0;0;-1)
(0;1;0)
Показати відповідь
В
Оскільки точка належить осі Оz, то в неї координати х та у дорівнюють 0. Так як точка лежить на додатному напряму осі Oz, то координата z в неї додатня. Маємо відповідь В.
Завдання 4. Знайдіть відстань від точки А (2;3;6) до осі Oz.
Оскільки точка належить осі Оz, то в неї координати х та у дорівнюють 0. Так як точка лежить на додатному напряму осі Oz, то координата z в неї додатня. Маємо відповідь В.
\sqrt{13}
7
6
5
3\sqrt{5}
Показати відповідь
А.
За малюнком відстань від точки А до осі Оz дорівнює проекції даного відрізка на площину Оху, тобто довжині діагоналі прямокутника зі сторонами 2 та 3. За теоремою Піфагора квадрат цього відрізка дорівнює 3² + 2² = 9 + 4 = 13. Отже шукана відстань дорівнює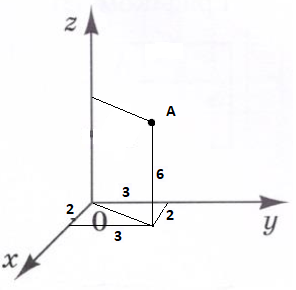 \sqrt{13}.
Завдання 5. У прямокутній системі координат у просторі знайдіть відстань від точки М(0;8;6) до осі Oу.
6
7
8
10
14
Показати відповідь
А
Так як перша координата точки М дорівнює 0, то точка лежить в площині Оуz. За малюнком відстань від точки М до осі Оу дорівнює 6.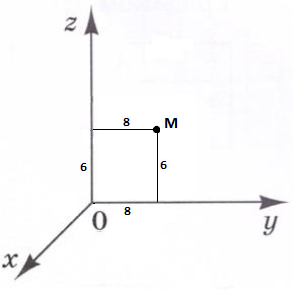
Завдання 6. Ортогональною проекцією відрізка з кінцями у точках А(-1;0;5) і В(-1;0;8) на координатну площину ху є:
пряма
промінь
відрізок
точка
фігура, що відрізняється від перелічених
Показати відповідь
Г
Так як координати х та у у кінців відрізка рівні, то він перпендикулярний до площини Оху і ортогональною проекцією на цю площину буде точка.
Так як координати х та у у кінців відрізка рівні, то він перпендикулярний до площини Оху і ортогональною проекцією на цю площину буде точка.
Рівняння сфери: сфера, з центром у точки О (хₒ;yₒ;zₒ) і радіусом R має рівняння (x-хₒ)² + (y-yₒ)² + (z-zₒ)² = R²
Завдання 7. У прямокутній системі координат у просторі задано сферу з центром у точці М. Відрізок АВ — діаметр цієї сфери. Визначте координати точки М, якщо А (2;-1;0), В (8;3;2).
(10;2;2)
(6;4;2)
(3;2;1)
(5;1;2)
(5;1;1)
Показати відповідь
Д.
Так як точка М - центр сфери, а АВ - її діаметр, то точка М - середина АВ. Маємо за формулами координат середини відрізка хM = (хA + хB):2 = (2 + 8):2 = 5, yM = (yA + yB):2 = (-1 + 3):2 = 1, zM = (zA + zB):2 = (0 + 2):2 = 1. Маємо точку (5;1;1).
Завдання 8. У прямокутній системі координат у просторі задано сферу із центром у початку координат, якій належить точка А (0;0;-5). Яка з наведених точок також належить цій сфері?
Так як точка М - центр сфери, а АВ - її діаметр, то точка М - середина АВ. Маємо за формулами координат середини відрізка хM = (хA + хB):2 = (2 + 8):2 = 5, yM = (yA + yB):2 = (-1 + 3):2 = 1, zM = (zA + zB):2 = (0 + 2):2 = 1. Маємо точку (5;1;1).
К(5;5;0)
L(0;1;4)
M(0;0;10)
N(0;0;5)
P(5;5;5)
Показати відповідь
Г.
Відстань від центра сфери до точки А дорівнює 5. Тоді сфері належать всі точки, відстань від яких до центра сфери (початку координат О(0;0;0)) дорівнює 5 (квадрат відстані дорівнює 25). Маємо:
KO² = (5-0)² + (5-0)² + (0-0)² = 25 + 25 = 50≠25
LO² = (0-0)² + (1-0)² + (4-0)² = 1 + 16 = 17≠25
MO² = (0-0)² + (0-0)² + (10-0)² = 100≠25
NO² = (0-0)² + (0-0)² + (5-0)² = 25
KO² = (5-0)² + (5-0)² + (5-0)² = 25 + 25 + 25 = 75≠25
Отже підходить лише точка N.
Завдання 9. На рисунку зображено прямокутну систему координат у просторі, на осях якої позначено точки K, L, M, N. Установіть відповідність між точками K, L, M, N (1-4) та їхніми можливими координатами (А-Д).
Відстань від центра сфери до точки А дорівнює 5. Тоді сфері належать всі точки, відстань від яких до центра сфери (початку координат О(0;0;0)) дорівнює 5 (квадрат відстані дорівнює 25). Маємо:
KO² = (5-0)² + (5-0)² + (0-0)² = 25 + 25 = 50≠25
LO² = (0-0)² + (1-0)² + (4-0)² = 1 + 16 = 17≠25
MO² = (0-0)² + (0-0)² + (10-0)² = 100≠25
NO² = (0-0)² + (0-0)² + (5-0)² = 25
KO² = (5-0)² + (5-0)² + (5-0)² = 25 + 25 + 25 = 75≠25
Отже підходить лише точка N.
1 К
2 L
3 M
4 N
2 L
3 M
4 N
А (-3;0;0)
Б (0;-3;0)
В (0;0;-3)
Г (0;0;3)
Д (0;3;0)
Б (0;-3;0)
В (0;0;-3)
Г (0;0;3)
Д (0;3;0)
Показати відповідь
1-Б, 2-Г, 3-А, 4-Д.
1) Точка К лежить на від’ємному напряму осі Оу, тому її координати по x і z дорівнюють 0, а у від’ємний. Точка (0;-3;0).
2) Точка L лежить на додатному напряму осі Оz, тому її координати по x і y дорівнюють 0, а z додатній. Точка (0;0;3).
3) Точка М лежить на від’ємному напряму осі Оx, тому її координати по y і z дорівнюють 0, а x від’ємний. Точка (-3;0;0) .
4) Точка N лежить на додатному напряму осі Оу, тому її координати по x і z дорівнюють 0, а у додатній. Точка (0;3;0).
Завдання 10. У прямокутній декартовій системі координат xyz у просторі задано точку М(1;-4;8). Установіть відповідність між початком речення (1-4) та його закінченням (А-Д) так, щоб утворилося правильне твердження.
1) Точка К лежить на від’ємному напряму осі Оу, тому її координати по x і z дорівнюють 0, а у від’ємний. Точка (0;-3;0).
2) Точка L лежить на додатному напряму осі Оz, тому її координати по x і y дорівнюють 0, а z додатній. Точка (0;0;3).
3) Точка М лежить на від’ємному напряму осі Оx, тому її координати по y і z дорівнюють 0, а x від’ємний. Точка (-3;0;0) .
4) Точка N лежить на додатному напряму осі Оу, тому її координати по x і z дорівнюють 0, а у додатній. Точка (0;3;0).
1 Відстань від точки М до площини ху дорівнює
2 Відстань від точки М до початку координат дорівнює
3 Відстань від точки М до осі z дорівнює
4 Відстань від точки М до точки N(1;0;8) дорівнює
2 Відстань від точки М до початку координат дорівнює
3 Відстань від точки М до осі z дорівнює
4 Відстань від точки М до точки N(1;0;8) дорівнює
А 1
Б 4
В \sqrt{17}
Г 8
Д 9
Б 4
В \sqrt{17}
Г 8
Д 9
Показати відповідь
1-Г, 2-Д, 3-В, 4-Б.
1) Відстань від точки до площини ху дорівнює модулю координати z. Отже відстань дорівнює 8.
2) MO² = (1-0)² + (-4-0)² + (8-0)² = 1 + 16 + 64 = 81. Отже МО = 9.
3) Відстань від точки М до осі Оz дорівнює проекції даного відрізка на площину Оху, тобто довжині діагоналі прямокутника зі сторонами 1 та 4. За теоремою Піфагора квадрат цього відрізка дорівнює 1² + 4² = 1 + 16 = 17. Отже шукана відстань дорівнює \sqrt{17}.
4) MN² = (1-1)² + (-4-0)² + (8-8)² = 0 + 16 + 0 = 16. Отже МО = 4.
1) Відстань від точки до площини ху дорівнює модулю координати z. Отже відстань дорівнює 8.
2) MO² = (1-0)² + (-4-0)² + (8-0)² = 1 + 16 + 64 = 81. Отже МО = 9.
3) Відстань від точки М до осі Оz дорівнює проекції даного відрізка на площину Оху, тобто довжині діагоналі прямокутника зі сторонами 1 та 4. За теоремою Піфагора квадрат цього відрізка дорівнює 1² + 4² = 1 + 16 = 17. Отже шукана відстань дорівнює \sqrt{17}.
4) MN² = (1-1)² + (-4-0)² + (8-8)² = 0 + 16 + 0 = 16. Отже МО = 4.
Коментарі